Üç rakam

Geçen hafta tekrar gündeme gelen nokta ızgaraları hakkında Salva Fuster şöyle diyor: "Bir nxn ızgarası için, kalemi kağıttan kaldırmadan veya aynı çizginin üzerinden iki kez 2(n-1) düz çizgiyle geçmeden tüm noktaları birleştirebileceğimizi söyleyebilirim; ancak 2x2 ızgarada üç çizgi gerekir. Ancak, daha az çizgiyle bunu yapmanın imkansız olduğunun gösterilmesi gerekir."

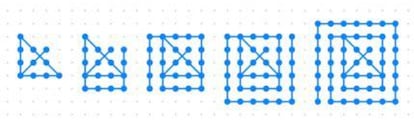
Bu arada, 4x4 ızgara için, şekilde gösterilenden farklı bir çözüm var; kesik çizginin birkaç köşesi ızgaranın dışında. Bulabilir misiniz? (İpucu: zarif ve simetrik bir çözüm.)

Ve dikdörtgen ve hareket eden parçalarla ilgili olarak Rafael Granero şöyle diyor: “C, uzun kenarının ortasına (AB'ye paralel) hareket eder.

B, C'nin olduğu kenarla aynı hizaya gelene kadar yeni AC çizgisine paralel hareket eder ve böylece C ile hizalanır. A, uzun kenarının yarısına gelene kadar BC çizgisine paralel hareket eder. Ve şimdi uzun kenarların yarısında A ve C noktalarına, Úbeda tepeleri boyunca da B noktalarına sahibiz."

Ve ne yaparsak yapalım B orada kalacaktır, çünkü üç parçayı dikdörtgenin üç kenarının orta noktalarına yerleştirmek imkansızdır. Köşelerden biri diğer ikisinin belirlediği doğruya paralel hareket ettiğinde, ABC üçgeninin alanı sabit kalır, çünkü ne tabanı ne de yüksekliği değişir ve değeri dikdörtgenin alanının yarısıdır. Köşeleri üç kenarın orta noktalarında olan bir üçgenin alanı ise dikdörtgenin alanının dörtte biri kadardır.

İç teğet çemberlerin yarıçapları ile ilgili olarak Luis Ortiz ustaca bir yaklaşım öneriyor: "Kenarları 3, 4 ve 5 olan bir üçgenin iç teğet çemberlerinin yarıçaplarının uzunlukları 2, 3 ve 6'dır; bu problem aşağıda denklemlerle çözülecektir. Üçgenin kenarları Pisagor teoremini sağlar, dolayısıyla dik üçgendir. Kenarlar, üçgenin köşelerinin şu koordinatlara sahip olduğu bir Kartezyen sisteminin x ve y eksenleriyle çakışacak şekilde tasarlanmıştır: A(0,0), B(4,0) ve C(0,3)". Buradan itibaren ispat basittir (yer darlığı nedeniyle tamamını dahil etmiyorum).

Her yerde daireler, üçgenler ve dikdörtgenler

Son haftalarda daireler, üçgenler ve dikdörtgenlerden bahsetmiştik. Bunlar, tesadüfen (ya da belki de değil) her yerde gördüğümüz üç geometrik şekildir.

Motorlu toplumumuzda her türlü taşıtta tekerleklerin bulunması, dairelerin baskınlığını açıklamaya yeter; ancak bunları kavanoz ve rögar kapakları veya kılıç bıçakları gibi birçok başka nesnede de görüyoruz.

Araç tekerleklerinin ve birçok kavanoz kapağının kendi kendine hizalı bir şekilde dönmeleri gerektiği için yuvarlak olması gerektiği aşikardır; ancak rögar kapakları kare, dikdörtgen veya eliptik olabilir... Ancak, dairesel olmalarının en az üç geçerli nedeni (kasıtlı bir kelime oyunu) vardır. Bu üç neden nedir? Yoksa üçten fazla mı?

Ve bıçaklı silahlar konusunda uzman olmaya gerek kalmadan, bir kılıç veya katana bıçağının eğriliğinin bir dairenin yayı olduğunu rahatlıkla söyleyebiliriz. Neden?

Üçgenlere gelince, onları elektrik hattı kulelerinden jeodezik kubbelere, hatta Eyfel Kulesi'nin kendisine kadar her türlü yapıda sürekli görmemizin ikna edici bir nedeni var (kasıtlı bir kelime oyunu). Peki bu ikna edici neden ne?

Kutuların, tuğlaların, duvarların, kağıtların ve daha birçok şeyin dikdörtgen (veya 3B'de aynı şey olan ortohedral) olması tesadüf değil; öyle ki Le Corbusier, dik açının doğayla dayanışma sözleşmemiz olduğunu söylemişti. Ne demek istiyordu?