O primeiro nem sempre vence

No jogo Penney, com o qual temos lidado nas últimas duas semanas , e como não existe um trio superior a todos os outros (é disso que se trata a não transitividade), é melhor escolher o segundo, porque, independentemente da escolha da outra pessoa, sempre haverá um trio com maior probabilidade de vencer. Em termos simples, é como se no jogo de pedra-papel-tesoura pudéssemos escolher sucessivamente em vez de simultaneamente: é óbvio que a pessoa que escolhesse o segundo sempre venceria.

No jogo de Penney, a estratégia do segundo jogador — sem garantia de sucesso, como no pedra-papel-tesoura, mas probabilisticamente mais favorável — é escolher o trio cujo primeiro termo é o oposto do segundo termo do trio do outro jogador, e cujos segundo e terceiro termos são, respectivamente, o primeiro e o segundo termos do trio do outro jogador. Por exemplo, se o primeiro jogador escolher o trio XXC, o segundo jogador deve escolher CXX. (Para melhorar a nota dele: mostre que esta é a melhor estratégia .)

Dados atípicos

Sobre os dados do Grime, Salva Fuster diz: “Se atribuirmos uma letra a cada dado:

A: 4 4 4 4 4 9

B: 3 3 3 3 8 8

C: 2 2 2 7 7 7

D: 1 1 6 6 6 6

E: 0 5 5 5 5 5

Temos que A vence B e C, mas perde para D e E; B vence C e D, mas perde para E e A; e assim por diante. Se desenharmos um pentágono com vértices A, B, C, D e E, cada vértice vence os dois seguintes e perde para os dois anteriores. Agora, não é exatamente uma vitória, mas há uma probabilidade maior de vitória . Por exemplo, o dado A vence B 26 vezes em comparação com 10, enquanto B vence C 24 vezes em comparação com 12. Se levarmos em conta a probabilidade de cada dado vencer ou perder contra os outros, mesmo que todos vençam contra dois e percam para os outros dois, eu diria que é melhor escolher o dado A ou D, pois eles têm uma probabilidade ligeiramente maior de vitória do que o resto dos dados.

Existem outros três dados não transitivos, tais que, em cada um deles, os pontos em suas faces somam 21, como nos dados convencionais, e, como estes, as pontuações variam de 1 a 6. E, como são dados não-T, cada dado vence um dos outros dois e perde para o outro. Quais números aparecem em suas faces?

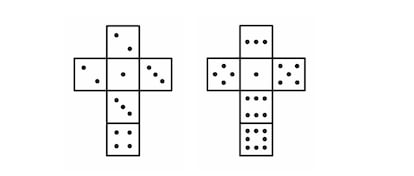
A respeito do dado de Sicherman , Bretos Bursó diz: “ Só há uma solução —além da usual: 123456, 123456— se impusermos que todas as faces tenham números positivos, mas se deixarmos alguma face ter 0 pontos há mais soluções: dada uma solução cujas faces mínimas são 1 e 1, se retirarmos um ponto de cada face de um dado e adicionarmos um ponto às faces do outro dado, resulta outra solução. Por exemplo, a solução usual resulta em 012345, 234567. Para obter a outra solução sem 0, parti das seguintes observações : as duas faces mínimas devem ser 1 e 1 e as duas faces máximas devem somar 12; em cada dado as faces mínima e máxima não podem ser repetidas; e a soma de todas as faces deve ser 42, de modo que as oito faces que não são nem mínimas nem máximas em cada dado devem somar 28.

A partir dessas observações obtemos a solução para o número: 122334, 134568. Você pode provar que ele é único?