No siempre gana el primero

En el juego de Penney, del que nos hemos ocupado las dos últimas semanas, y puesto que no hay una terna superior a todas las demás (en eso consiste la no transitividad), conviene elegir en segundo lugar, pues, elija lo que elija el otro, siempre habrá una terna con más probabilidades de ganar. Simplificando, es como si en el juego de piedra-papel-tijera pudiéramos elegir de forma sucesiva en vez de simultánea: es evidente que el segundo en elegir ganaría siempre.

En el juego de Penney, la estrategia del segundo jugador —no de éxito seguro, como en el piedra-papel-tijera, pero sí probabilísticamente más favorable— consiste en elegir la terna cuyo primer término es el contrario del segundo de la terna del otro jugador, y cuyos segundo y tercer término son, respectivamente, el primero y el segundo del otro. Por ejemplo, si el primer jugador elige la terna XXC, el segundo debe elegir CXX. (Para subir nota: demuestra que esta es la mejor estrategia).

Con respecto a los dados de Grime, dice Salva Fuster: “Si asignamos una letra a cada dado:

A: 4 4 4 4 4 9

B: 3 3 3 3 8 8

C: 2 2 2 7 7 7

D: 1 1 6 6 6 6

E: 0 5 5 5 5 5

Tenemos que A gana a B y a C, pero pierde con D y E; B gana a C y D, pero pierde con E y A; y así sucesivamente. Si dibujamos un pentágono con vértices A, B, C, D y E, cada vértice gana a los dos siguientes y pierde con los dos anteriores. Ahora bien, no se gana exactamente, sino que hay una probabilidad mayor de ganar. Por ejemplo, el dado A gana al B en 26 casos frente a 10, mientras que B gana a C en 24 casos frente a 12. Si tenemos en cuenta la probabilidad de ganar o perder de cada dado frente a otros, a pesar de que todos ganen a dos y pierdan con otros dos, yo diría que conviene elegir los dados A o D, pues tienen una probabilidad de ganar ligeramente mayor que el resto de los dados.

Hay otros tres dados no transitivos, tales que, en cada uno de ellos, los puntos de sus caras suman 21, como en los dados convencionales, y, como en estos, las puntuaciones van del 1 al 6. Y, puesto que son dados no-T, cada dado gana a uno de los dos restantes y pierde con el otro. ¿Qué números figuran en sus caras?

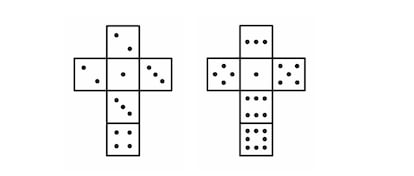
Con respecto a los dados de Sicherman, dice Bretos Bursó: “Hay una única solución —aparte de la habitual: 123456, 123456— si imponemos que todas las caras tengan numeración positiva, pero si dejamos que alguna cara tenga 0 puntos hay más soluciones: dada una solución cuyas caras mínimas son 1 y 1, si a cada cara de un dado le quitamos un punto y a las del otro dado le añadimos un punto resulta otra solución. Por ejemplo, de la solución habitual resulta la solución 012345, 234567. Para obtener la otra solución sin 0, he partido de las siguientes observaciones: las dos caras mínimas deben ser 1 y 1 y las dos caras máximas deben sumar 12; en cada dado las caras mínima y máxima no pueden repetirse; y la suma de todas las caras debe ser 42, con lo que las ocho caras que no son mínima ni máxima en cada dado deben sumar 28.

A partir de estas observaciones se obtiene la solución de la figura: 122334, 134568. ¿Puedes demostrar que es única?