Le tre figure

Riguardo alle griglie di punti, un tema ricorrente emerso anche la scorsa settimana, Salva Fuster afferma: "Direi che per una griglia nxn possiamo unire tutti i punti senza staccare la matita dal foglio o ripassare la stessa linea due volte con 2(n-1) linee rette, tranne nel caso della griglia 2x2, che richiederebbe tre linee. Tuttavia, bisognerebbe dimostrare che è impossibile farlo con meno linee".

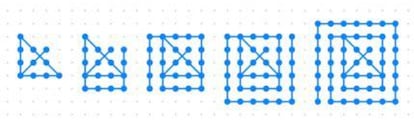
A proposito, per la griglia 4x4 esiste una soluzione diversa da quella mostrata in figura, con diversi vertici della linea spezzata all'esterno della griglia. Riesci a trovarla? (Suggerimento: è un'elegante soluzione simmetrica.)

E riguardo al rettangolo e ai pezzi in movimento, Rafael Granero dice: “C si sposta al centro del suo lato lungo (parallelo ad AB).

B si muove parallelamente alla nuova linea AC finché non è a livello del lato dove si trova C, allineandosi così con C. A si muove parallelamente alla linea BC finché non è a metà del suo lato lungo. E ora abbiamo i punti A e C a metà dei lati lunghi, e B lungo le colline di Úbeda."

E B rimarrà lì qualunque cosa facciamo, poiché è impossibile posizionare i tre pezzi nei punti medi di tre lati del rettangolo. Quando uno dei vertici si muove parallelamente alla linea determinata dagli altri due, l'area del triangolo ABC rimane costante, poiché né la base né la lunghezza dell'altezza variano, e il suo valore è 1/2 dell'area del rettangolo, mentre l'area di un triangolo con i vertici nei punti medi di tre lati sarebbe 1/4 di quella del rettangolo.

Per quanto riguarda i raggi delle circonferenze esinscritte, Luis Ortiz propone un approccio ingegnoso: "I raggi delle circonferenze esinscritte di un triangolo di lati 3, 4 e 5 hanno lunghezze di 2, 3 e 6, un problema che verrà risolto più avanti mediante equazioni. I lati del triangolo soddisfano il teorema di Pitagora, quindi è un triangolo rettangolo. I cateti sono fatti coincidere con gli assi x e y di un sistema cartesiano, in modo che i vertici del triangolo abbiano le seguenti coordinate: A(0,0), B(4,0) e C(0,3)". Da qui in poi, la dimostrazione è semplice (non la includo per intero per motivi di spazio).

Cerchi, triangoli e rettangoli ovunque

Nelle ultime settimane abbiamo parlato di cerchi, triangoli e rettangoli che, guarda caso (o forse no), sono le tre figure geometriche che vediamo ovunque.

L'onnipresenza delle ruote su tutti i tipi di veicoli nella nostra società motorizzata sarebbe sufficiente a spiegare la predominanza dei cerchi; ma li troviamo anche su molti altri oggetti, come coperchi di barattoli e tombini o lame di sciabola.

È ovvio che le ruote dei veicoli e i coperchi di molti barattoli devono essere rotondi, poiché devono ruotare in modo autoallineato; ma i tombini potrebbero essere quadrati, rettangolari o ellittici... Tuttavia, ci sono almeno tre valide ragioni (gioco di parole voluto) per cui dovrebbero essere circolari. Quali sono queste tre ragioni? O ce ne sono più di tre?

E senza bisogno di essere esperti di armi bianche, possiamo tranquillamente affermare che la curvatura della lama di una sciabola o di una katana è un arco di cerchio. Perché?

Per quanto riguarda i triangoli, c'è una ragione convincente (gioco di parole voluto) per cui li vediamo costantemente in ogni tipo di struttura, dai tralicci delle linee elettriche alle cupole geodetiche, inclusa la Torre Eiffel stessa. Qual è questa ragione convincente?

E non è un caso che scatole, mattoni, muri, fogli di carta e tante altre cose siano rettangolari (o ortoedriche, che è la stessa cosa in 3D), al punto che Le Corbusier disse che l'angolo retto è il nostro patto di solidarietà con la natura. Cosa intendeva dire?